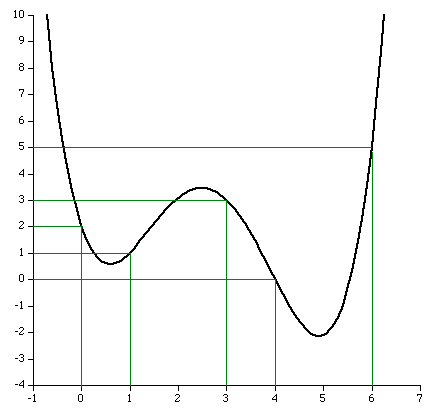
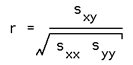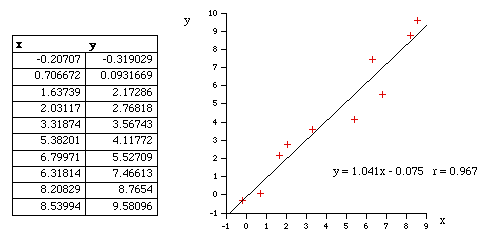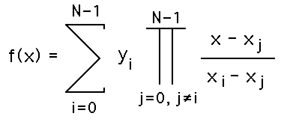아~ 띠바... 그동안 Visual Studio의 출력창의 Debug 출력에서 징그럽게 날 괴롭히던 넘을 찾았다...
바로 "ImageSafer" ....
이놈이 왜 있는지는 자세히 기억이 나질 않는다....
다만....
아래와 같이 디버그모드 실행시... 나타나던....그 넘들...
Snap Text lang[??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????] LangiD 0x0000
ParseSnapTexts[본 화면은 보안 정책에 의하여 보호되었습니다.]
Snap Text lang[??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????] LangiD 0x0000
ParseSnapTexts[It is Protected by the policy of MarkAny Inc.]
Snap Text lang[??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????] LangiD 0x0000
ParseSnapTexts[본 화면은 보안 정책에 의하여 보호되었습니다.]
Snap Text lang[??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????] LangiD 0x0000
ParseSnapTexts[It is Protected by the policy of MarkAny Inc.]
ApiHook Class Init before
Protection Manager Set[3971020]
CHookFunc() Share Init
IMGSF01-Init API
CGlobalValMgr: Init 1
Mutext Name [{7E1E6616-942F-41fe-A6A2-ADF0A213490E}-S1]
Mutex Create[208] Err[183]
Mutext Name [{402B3B89-13A1-4c6f-9E02-8518F425A6E4}-S1]
Mutex Create[20c] Err[183]
Vista
ShrareMem Name [{F180788B-0646-4218-92F1-79015DC43882}-S1]
WinVista High
CreateShMem1111111111111 [1] err[183]
CreateShMem1111111111111 [1] err[183]
CreateShMem : CreateFileMapping - m_hMem [0x210]
CreateShMem : MapViewOfFile - m_pData [0x40c0000]
CreateShMem : OK
Init : CreateShMem [1]
CProtectionMgr::SetShareMem[3971020]
ApiHook Class Init After
ApiHook Detours Attach
MyDetourAttach[0]
BitBlt Hook
MyDetourAttach[0]
StretchBlt Hook
MyDetourAttach[0]
GetClipboardData Hook
GetClipboardData[764e9f1d]
MSIMG [72eb1320]
MyDetourAttach[0]
TransparentBlt Hook
TransparentBlt[72eb1320]
PrintWindow Org [7650882b]
MyDetourAttach[0]
PrintWindow Hook
MaGetExeInfo : szExe
MaGetExeInfo : [\StringFileInfo\041204b0\ProductName]
MaGetExeInfo : Name [TODO: <제품 이름>]
MaGetExeInfo : [\StringFileInfo\041204b0\FileVersion]
MaGetExeInfo : Version [1.0.0.1]
MaGetExeInfo : [\StringFileInfo\041204b0\FileDescription]
Special Logic[0]
특히.....
★★★★★DK_TransparentBlt Source Type [10]
★★★★★DK_TransparentBlt Source Type [10]
★★★★★DK_TransparentBlt Source Type [10]
★★★★★DK_TransparentBlt Source Type [10]
★★★★★DK_TransparentBlt Source Type [10]
★★★★★DK_TransparentBlt Source Type [10]
★★★★★DK_TransparentBlt Source Type [10]
징그럽게 지속적으로 나와 디버깅 메시지보기를 어렵게 맹글었던...
★★★★★DK_TransparentBlt Source Type [10].... 출력....
이것이 없어졌다....
Windows 서비스 대화창에서
서비스 이름: Image Protection
표시이름: Image Protect Service
설명 : ImageSAFER 4.0 Service
실행파일 경로 : C:\Windows\ImageSAFERSvc.exe
이놈을 죽였더니...
쾌지나 칭칭나네~~~~ 아싸 가오리~~~
위의 그 징그럽던 출력들이 없어졌다.... 좋아좋아~~~~
긴긴 삽질이 막을 내렸다....
'삽질' 카테고리의 다른 글
| TableSpace와 관련된 DataDictionary View (0) | 2012.02.03 |
|---|---|
| [펌]테이블/ 테이블스페이스별 사용량 확인 (0) | 2012.02.03 |
| std::remove_if .... (0) | 2011.11.06 |
| image 포맷 변환. (0) | 2011.11.04 |
| ImageCodecInfo Class (0) | 2011.11.04 |

 zImageCvt.exe
zImageCvt.exe zImageCvt.cpp
zImageCvt.cpp